Все, что касается расчета среднего направления ветра

Для расчета среднего направления ветра необходимо иметь данные о направлении ветра за определенный период времени. Эти данные могут быть получены из метеорологических наблюдений или из других источников, таких как архивные данные или прогнозы погоды.

Сбор данных о направлении ветра: Соберите данные о направлении ветра в градусах (например, от 0 до 360 градусов) за выбранный период времени (например, за месяц или год).

Подсчет количества случаев каждого направления: Подсчитайте количество случаев для каждого направления ветра (например, 10 случаев ветра с направлением 20 градусов, 5 случаев ветра с направлением 45 градусов и т.д.).

Определение среднего направления ветра: Для определения среднего направления ветра можно использовать различные методы, такие как:

• Метод среднего арифметического: Вычислите среднее арифметическое всех направлений ветра. Это даст вам среднее направление ветра без учета частоты появления каждого направления.
• Метод взвешенного среднего: Умножьте каждое направление на его частоту появления и вычислите сумму всех произведений. Затем разделите эту сумму на общее количество случаев. Этот метод учитывает частоту появления каждого направления и дает более точное представление о среднем направлении ветра.

1. Интерпретация результатов: После расчета среднего направления ветра вы можете интерпретировать результаты в соответствии с вашими потребностями. Например, если среднее направление ветра составляет 270 градусов (северо-запад), это означает, что ветер чаще всего дует с северо-запада.

Обратите внимание, что точность расчета среднего направления ветра зависит от качества и количества собранных данных. Если данные содержат ошибки или пропуски, то результаты могут быть неточными. Также важно учитывать, что среднее направление ветра может меняться в зависимости от времени года, местоположения и других

Расчет среднего направления ветра методом взвешенного среднего

Для расчета среднего направления ветра с использованием метода взвешенного среднего необходимо выполнить следующие шаги:

Сбор данных о направлении ветра:

• Соберите данные о направлении ветра за определенный период времени (например, за месяц или год). Данные могут быть представлены в виде таблицы или графика.
• Для каждого периода времени определите направление ветра в градусах (от 0 до 360 градусов).

Определение весов для каждого направления:

• Определите веса для каждого направления ветра. Веса могут быть пропорциональны частоте появления данного направления ветра или другим параметрам, которые вы считаете важными.

Расчет взвешенного среднего:

• Рассчитайте среднее направление ветра, используя формулу взвешенного среднего:
  $\bar{x} = \frac{\sum_{i=1}^{n} w_i x_i}{\sum_{i=1}^{n} w_i}$, где:
  - $\bar{x}$ - среднее направление ветра;
  - $w_i$ - вес для направления $x_i$;
  - $x_i$ - направление ветра для периода $i$.

Интерпретация результатов:

• Проанализируйте полученное среднее направление ветра и его значение. Это может помочь вам понять общие тенденции в направлении ветра на данной территории.

Обратите внимание, что этот метод может быть адаптирован под конкретные условия и требования. Также важно учитывать точность и надежность данных, используемых для расчета.

Пример расчета:

Предположим, у нас есть следующие данные о направлениях ветра за 5 дней:

День	Направление ветра (градусы)
1	20
2	40
3	80
4	120
5	240

Пусть веса для каждого дня равны 1 (т.е. все направления имеют одинаковый вес). Тогда среднее направление ветра будет равно:
$\bar{x} = \frac{(20 + 40 + 80 + 120 + 240)}{5} = 96$ градусов.

Это означает, что среднее направление ветра за эти 5 дней составляет примерно 96 градусов

Расчет среднего направления ветра

Для расчета среднего направления ветра необходимо учитывать, что направление ветра является циклической величиной, то есть изменяется по кругу от 0 до 360 градусов. Прямое вычисление среднего арифметического для таких величин может привести к некорректным результатам.

Для расчета среднего направления ветра используется следующий алгоритм:

1. Перевести направления ветра в радианы:
   Направление в радианах = Направление в градусах * π / 180

2. Вычислить средние значения косинуса и синуса направлений ветра:
   Средний косинус = Σcos(направление) / n
   Средний синус = Σsin(направление) / n

3. Вычислить среднее направление ветра в радианах:
   Среднее направление в радианах = atan2(средний синус, средний косинус)

4. Перевести результат из радиан в градусы:
   Среднее направление в градусах = среднее направление в радианах * 180 / π

Например, если имеются следующие измерения направления ветра:
[10°, 20°, 30°, 340°, 350°]

Тогда:
1. Направления в радианах:
   [10°, 20°, 30°, 340°, 350°] = [0.175, 0.349, 0.524, 5.930, 6.109] радиан

2. Вычисление средних значений косинуса и синуса:
   Средний косинус = (cos(0.175) + cos(0.349) + cos(0.524) + cos(5.930) + cos(6.109)) / 5 = 0.766
   Средний синус = (sin(0.175) + sin(0.349) + sin(0.524) + sin(5.930) + sin(6.109)) / 5 = 0.643

3. Вычисление среднего направления в радианах:
   Среднее направление в радианах = atan2(0.643, 0.766) = 0.739 радиан

4. Перевод в градусы:
   Среднее направление в градусах = 0.739 * 180 / π = 42.3°

Таким образом, среднее направление ветра для данного примера составляет 42.3 градуса.

 

Расчет среднеквадратичного отклонения (СКО) для направления ветра

Для расчета среднеквадратичного отклонения (СКО) для направления ветра можно использовать следующую формулу:

СКО = sqrt(Σ(x - μ)^2 / n)

где:

- x - значение направления ветра

- μ - среднее значение направления ветра

- n - количество измерений

Вот пошаговый алгоритм расчета:

1. Вычислить среднее значение направления ветра:

   μ = Σx / n

2. Для каждого измерения направления ветра x, вычислить отклонение от среднего значения:

   (x - μ)

3. Возвести каждое отклонение в квадрат:

   (x - μ)^2

4. Сложить все квадраты отклонений:

   Σ(x - μ)^2

5. Разделить сумму квадратов отклонений на количество измерений n:

   Σ(x - μ)^2 / n

6. Взять квадратный корень из полученного значения:

   sqrt(Σ(x - μ)^2 / n)

Результатом будет значение среднеквадратичного отклонения для направления ветра.

Например, если у нас есть измерения направления ветра: 

[10, 15, 20, 25, 30] 

Тогда:

- Среднее значение μ = (10 + 15 + 20 + 25 + 30) / 5 = 20

- Отклонения: (10 - 20)^2 = 100, (15 - 20)^2 = 25, (20 - 20)^2 = 0, (25 - 20)^2 = 25, (30 - 20)^2 = 100

- Сумма квадратов отклонений: 100 + 25 + 0 + 25 + 100 = 250

- СКО = sqrt(250 / 5) = sqrt(50) = 7.07

Таким образом, среднеквадратичное отклонение направления ветра для данного примера равно 7.07 градусов.

 

Второй вариант

Расчет среднеквадратичного отклонения для направления ветра проводился по формуле: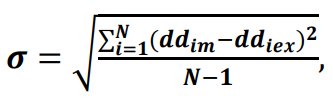

где ddm− модельные значения направления ветра, ddex−экспериментальные значения скорости ветра, N – количество равноотстоящих отсчетов для дискретных данных направления ветра).

 

Расчет среднеквадратичного отклонения (СКО) для скорости ветра

Для расчета среднеквадратичного отклонения (СКО) для скорости ветра можно использовать аналогичную формулу:

СКО = sqrt(Σ(x - μ)^2 / n)

где:

- x - значение скорости ветра

- μ - среднее значение скорости ветра

- n - количество измерений

Вот пошаговый алгоритм расчета:

1. Вычислить среднее значение скорости ветра:

   μ = Σx / n

2. Для каждого измерения скорости ветра x, вычислить отклонение от среднего значения:

   (x - μ)

3. Возвести каждое отклонение в квадрат:

   (x - μ)^2

4. Сложить все квадраты отклонений:

   Σ(x - μ)^2

5. Разделить сумму квадратов отклонений на количество измерений n:

   Σ(x - μ)^2 / n

6. Взять квадратный корень из полученного значения:

   sqrt(Σ(x - μ)^2 / n)

Результатом будет значение среднеквадратичного отклонения для скорости ветра.

Например, если у нас есть измерения скорости ветра:

[5, 7, 9, 11, 13] м/с

Тогда:

- Среднее значение μ = (5 + 7 + 9 + 11 + 13) / 5 = 9 м/с

- Отклонения: (5 - 9)^2 = 16, (7 - 9)^2 = 4, (9 - 9)^2 = 0, (11 - 9)^2 = 4, (13 - 9)^2 = 16

- Сумма квадратов отклонений: 16 + 4 + 0 + 4 + 16 = 40

- СКО = sqrt(40 / 5) = sqrt(8) = 2.83 м/с

Таким образом, среднеквадратичное отклонение скорости ветра для данного примера равно 2.83 м/с.

 

Второй вариант
Расчет среднеквадратичного отклонения для скорости ветра проводился по формуле: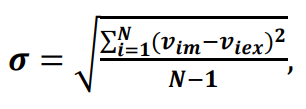

где vm− модельные значения скорости ветра, vex− экспериментальные значения скорости ветра, N – количество равноотстоящих отсчетов для дискретных данных направления ветра).